Case Study: Map Reduce

Map Reduce Explained

MapReduce is a programming model for processing and generating big data sets with a parallel, distributed algorithm on a cluster. Let’s explain it here as a way to parallelize sandwich making.

Map reduce is a function that

1. chunks the input,
2. maps a function over the chunks in parallel, and
3. reduces the results to a single value.

Figure 1.1: MapReduce to make sandwich.

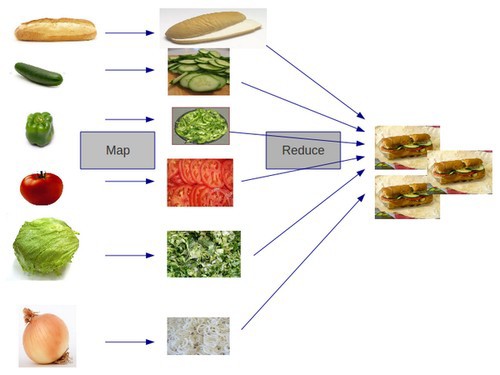
Map Reduce “Library” Functions:

The Haskell definitions of mapReduce functions, reflected:

Of course, for mapReduce to be efficient the map function should be parallelized, e.g., using parMap.

Map Reduce “Client” Functions: Summing a List

Let’s assume that sum is the standard list summing and psum is the mapReduce parallel summing.

Can we prove that sum and psum are equivalent?

Proving Code Equivalence: sum and psum

The equivalence proof is an instance of the higher order theorem mRTheorem:

Chunk Definition:

First, let’s define the chunk function that splits a list into chunks of size n.

Question: Define the take and drop functions below that satisfy the following specifications:

Question: Define the chunk function below that splits a list into chunks of size n.

drop :: Int -> [a] -> [a]
drop 0 x = x 
drop i (x:xs) = drop (i-1) xs 

take 0 _ = []
take i (x:xs) = x : take (i-1) xs

{-@ chunk :: Int -> x:[a] -> [[a]] / [len x] @-}
chunk :: Int -> [a] -> [[a]]
chunk i x 
  | i <= 0 || length x <= i = [x]
  | otherwise = take i x : chunk i (drop i x)

Higher Order Theorem: mRTheorem

The higher order theorem mRTheorem states that:

If f is right identity and op is distributive, then mapReduce is equivalent to sequential.

Question: What is the proof of mRTheorem?

mRTheorem n f op rightId distrib is 
  | n <= 0 || length is <= n 
  =   mapReduce n f op is 
  === reduce op (f []) (map f (chunk n is))
  === reduce op (f []) [f is]
  ? rightId is
  === f is 
  *** QED 

mRTheorem n f op rightId distrib is  
  =   mapReduce n f op is 
  === reduce op (f []) (map f (chunk n is))
  === reduce op (f []) (map f (take n is : chunk n (drop n is)))
  === reduce op (f []) (f (take n is) : map f (chunk n (drop n is)))
  ===  op (f (take n is)) (reduce op (f []) (map f (chunk n (drop n is))))
  ? mRTheorem n f op rightId distrib (drop n is)
  === op (f (take n is)) (f (drop n is))
  ? distrib (take n is) (drop n is)
  === f (take n is ++ drop n is)
   ? takeDrop n is
  === f is   
  *** QED  

takeDrop :: Int -> [a] -> Proof
{-@ takeDrop :: i:Nat -> xs:{[a] | i <= len xs }
             -> {take i xs ++ drop i xs == xs} @-}
takeDrop 0 xs     = ()
takeDrop n (_:xs) = takeDrop (n-1) xs

Lemmata for mRTheorem on plus

Question: What is the proof of plusRightId?

plusRightId []     = ()
plusRightId (x:xs) = plusRightId xs 

Question: What is the proof of sumDistr?

sumDistr [] ys = ()
sumDistr (x:xs) ys = sumDistr xs ys  

Summary

We saw a case study in which map reduce is used to parallelize the sum of a list. Using Liquid Haskell, we can prove that the parallel sum is equivalent to the sequential sum.

Appendix: List Manipulation Functions