Type Classes
> {-# LANGUAGE FlexibleInstances #-}
> module TypeClasses whereWe have already seen that the (<) operator works for a bunch of different underlying data types. For example
ghci> 2 < 3
True
ghci> 3.9 < 3.5
False Similarly we can compare all sorts of values
ghci> 2 == 3
False
ghci> [2.9, 3.5] == [2.9, 3.5]
True“So?” Indeed, this is quite unremarkable, since languages since the dawn of time has supported some form of operator “overloading” to support this kind of ad–hoc polymorphism.
However, in Haskell, there is no caste system. There is no distinction between operators and functions. All are first class citizens in Haskell.
Well then, what type do we give to functions like (<) and (==)? Something like
(<) :: Integer -> Integer -> Bool would be too anemic, since we want to add two doubles as well! Can type variables help?
(<) :: a -> a -> BoolNope. Thats a bit too aggressive, since it doesn’t make sense, to compare two functions with each other! Haskell solves this problem with an insanely slick mechanism called typeclasses, introduced by Wadler and Blott.
Qualified Types
To see the right type, lets just ask
ghci> :type (<)
(<) :: Ord a => a -> a -> BoolWe call the above a qualified type. Read it as, (<) takes in two a values and returns an Bool, for any type a that is an Ord.
The name Ord can be thought of as a predicate over types. Some types satisfy the Ord predicate. Examples include Integer, Double etc, and any values of those types can be passed to (<). Other types do not satisfy the predicate. Examples include functions etc, and so values of those types cannot be passed to (<).
ghci> id < flip
<interactive>:15:1: error:
• No instance for (Ord ((a0 -> a0 -> c0) -> a0 -> a0 -> c0))
arising from a use of ‘<’
(maybe you haven't applied a function to enough arguments?)
• In the expression: id < flip
In an equation for ‘it’: it = id < flipNow these kinds of error messages make sense. Basically Haskell is complaining that function types are not an instance of Ord.
OK, SO WHAT IS A TYPECLASS?
In a nutshell, a typeclass is a collection of operations (functions) that must exist for the underlying type. For example, lets look at possibly the simplest typeclass Eq
class Eq a where
(==) :: a -> a -> Bool
(/=) :: a -> a -> BoolThat is, a type a can be an instance of Eq as long as there are two functions that determine if two a values are respectively equal or disequal. Similarly, the typeclass Show captures the requirements that make a particular datatype be viewable,
class Show a where
show :: a -> StringIndeed, we can test this on different (built-in) types
ghci> show 2
"2"
ghci> show 3.14
"3.14"ghci> show (1, "two", ([],[],[]))
"(1,\"two\",([],[],[]))"When we type an expression into ghci, it computes the value and then calls show on the result. Thus, if we create a new type by
ghci> data Unshowable = A | B | Cthen we can create values of the type,
ghci> let x = A
ghci> :type x
x :: Unshowablebut can’t view or compare them
ghci> x = A
<interactive>:1:0:
No instance for (Show Unshowable)
arising from a use of `print' at <interactive>:1:0
Possible fix: add an instance declaration for (Show Unshowable)
In a stmt of a 'do' expression: print it
ghci> x == x
<interactive>:1:0:
No instance for (Eq Unshowable)
arising from a use of `==' at <interactive>:1:0-5
Possible fix: add an instance declaration for (Eq Unshowable)
In the expression: x == x
In the definition of `it': it = x == xAgain, the previously incomprehensible type error message should make sense to you.
Q: Lets create an instance for Show Unshowable.
AUTOMATIC DERIVATION
Of course, this is lame; we should be able to compare and view them. To allow this, Haskell allows us automatically derive functions for certain key type classes, namely those in the standard library.
To do so, we simply dress up the data type definition with
> data Showable = A' | B' | C' deriving (Eq, Show)and now we have
ghci> let x' = A'
ghci> :type x'
x' :: Showable
ghci> x'
A'
ghci> x' == x'
TrueSTANDARD TYPECLASS HIERARCHY
Let us now peruse the definition of the Ord typeclass.
ghci> :info Ord
class Eq a => Ord a where
compare :: a -> a -> Ordering
(<) :: a -> a -> Bool
(<=) :: a -> a -> Bool
(>) :: a -> a -> Bool
(>=) :: a -> a -> Bool
max :: a -> a -> a
min :: a -> a -> a
{-# MINIMAL compare | (<=) #-}There’s quite a bit going on there. A type a can only be deemed an instance of Ord if
- The type is also an instance of
Eq, and - There are functions for ordering values of that type.
In other words in addition to the ordering operations, we can compare check equality on two Ord values.
Haskell comes equipped with a rich set of built-in classes.
Standard Typeclass Hierarchy
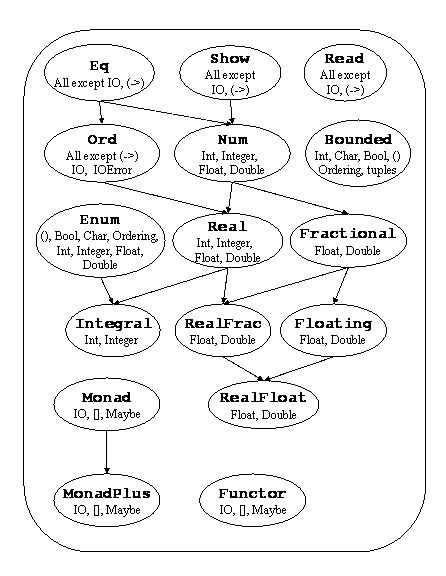
alt text
In the above picture, there is an edge from Eq to Ord because for something to be an Ord it must also be an Eq. There are a few other ones that we will come to know (and love!) in due course…
Most of these type classes come with default instances for the basic types. But not all of them
Q: Why does Haskell reject the following expression?
(1,2,3,4,5,6,7,8,9,10,1,1,1,1,1,1) == (1,2,3,4,5,6,7,8,9,10,1,1,1,1,1,1)> instance (Eq a, Eq b, Eq c, Eq d, Eq e, Eq f, Eq g, Eq h, Eq i,
> Eq j, Eq k, Eq l, Eq m, Eq n, Eq o, Eq w) =>
> Eq (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, w) where
> _ == _ = False Using Typeclasses
We have already see how type classes integrate with the rest of the Haskell’s type.
Recall the insert function
> insert x [] = [x]
> insert x (y:ys)
> | x <= y = x:y:ys
> | otherwise = y:insert x ysNotice that we didn’t write down the type of the insert. Lets see what the type is
<ghci :t insert
insert :: Ord t => t -> [t] -> [t]How, did the engine figure this out? Easy enough, if you look at the body of the insert, you’ll see that we compare two key values.
Constraint Propagation
Every function that calls insert should propagate the Ord constraint.
> insertSort :: Ord a => [a] ->[a]
> -- insertSort ::[Int] ->[Int]
> insertSort = foldl (flip insert) []
>
> f :: Int -> Int
> f x = x Note, that now Haskell is not smart enough to figure out the constraint, so we need an explicit type signature.
Explicit Signatures
In the case of insertSort Haskell could have guessed a proper type. But, there are cases when the use of type classes requires explicit annotations (which change the behavior of the code.)
For example, Read is a built-in typeclass, where any instance a of Read has a function
read :: (Read a) => String -> awhich can parse a string and turn it into an a. Thus, Read is, in a sense, the dual of the Show.
Q: Is it possible that read creates any value of type a? Does this remind you any function we saw earlier?
Q: What does the expression read "2" evaluate to?
Haskell is foxed, because it doesn’t know what to convert the string to! Did we want an Int or a Double? Or maybe something else altogether. Thus, we get back the complaint
interactive>:1:0:
Ambiguous type variable `a' in the constraint:
`Read a' arising from a use of `read' at <interactive>:1:0-9
Probable fix: add a type signature that fixes these type variable(s)which clearly states what the issue is. Thus, here an explicit type annotation is needed to tell it what to convert the string to. Thus, if we play nice and add the types we get
ghci> (read "2") :: Int
2ghci> (read "2") :: Float
2.0Note the different results due to the different types.
Instantiating Typeclasses
So far we have seen Haskell’s nifty support for overloading by observing that
some standard types are instances of standard type classes, and
new types can be automatically made instances of standard type classes.
However, in many situations the automatic instantiation doesn’t quite cut it, and instead we need to (and get to!) create our own instances.
For example suppose you want to compare two tic-tac-toe tiles.
> data Tile = X | O | EmptyTile
> -- deriving (Eq)Q: What does
ghci> EmptyTile == EmptyTile evaluate to?
The equality test is structural, as in, a data type is always equal to itself.
What is we want to define tile-equality so that comparison with EmptyTile is always False?
We can write our own tile-equality operator to capture exactly this crazy requirement.
> instance Eq Tile where
> X == X = True
> O == O = True
> _ == _ = False Q: Now what does
ghci> EmptyTile == EmptyTile evaluate to?
How about
ghci> EmptyTile /= EmptyTile To undertand how, (/=) is evaluated let us look at the full definition of the Eq typeclass. Ah! the typeclass definition also provides default implementations of each operation (in terms of the other operation.) Thus, all we need to do is define (==) and we will get (/=) (not-equals) for free!
In general, when instantiating a typeclass, Haskell will check that we have provided a minimal implementation containing enough functions from which the remaining functions can be obtained (via their default implementations.)
Laws
In addition to the explicit type requirements, a typeclass also encodes a set of laws that describe the relationships between the different operations. For example, the intention of the Eq typeclass is that the supplied implementations of (==) and (/=) satisfy the law
forall t1 t2, t1 == t2 <==> not t1 /= t2
forall t1, t1 == t1 Unfortunately, there is no way for Haskell to verify that your implementations satisfy the laws, so this is something to be extra careful about, when using typeclasses.
Type classes are interfaces
Many of you might have experience with object-oriented programming languages like Java. You are in danger! Do not fall in the trap of confusing type classes (in Haskell) with classes (in Java)! They are not very similar, and you do not use them to solve the same problems.
If anything, type classes correspond to interfaces in Java: Both contain methods without implementation and their type signatures, and instances provide the implementation.
Classes and objects as in Java do not have a direct correspondence in Haskell, and that is ok, because problems are approached differently. But the Interaction type that we defined last week is, in some sense, an approximation of a class. The concrete Interactions that we defined are instances of this class, and functions like withStartScreen relate to inheritance (or maybe ot the decorator pattern).
Internals of Type classes
Type classes define interfaces that in Haskell’s terms are called dictionaries.
For instance, from the Ord class definition the compiler will create a dictionary that stores all the class methods. This dictionary will be just a data type with one field per each defined method:
> data OrdDict a
> = OrdDict { leq :: a -> a -> Bool
> , gt :: a -> a -> Bool
> }This dictionary will be an implicit argument to all the functions that use the class methods. The implicit argument will be automatically filled in by the compiler.
The compiler will transform our insert function to a function that takes an extra explicit dictionary argument and use this argument to compare values of type a.
> insert' dict x [] = [x]
> insert' dict x (y:ys)
> | leq dict x y = x:y:ys
> | otherwise = y:insert' dict x ys
>
> insertSort' :: OrdDict a -> [a] ->[a]
> insertSort' dict = foldl (flip (insert' dict)) []
>
>
> insertSort' :: Ord a => [a] ->[a]
> insertSort' = foldl (flip (insert)) [] Note how insertSort' propagates the dictionary to insert'.
When we define instances of the Ord class we basically define dictionary values.
> intDict :: OrdDict Int
> intDict = OrdDict (<=) (>)Then, the compiler together with the type inferences figure out how to properly pass around these dictionaries.
> insertInt :: [Int]
> insertInt = insertSort' intDict [4, 3, 6, 2, 9]Creating Typeclasses
It turns out that typeclasses are useful for many different things. We will see some of those over the next few lectures, but let us conclude today’s class with a quick example that provides a (very) small taste of their capabilities.
JSON
JavaScript Object Notation or JSON is a simple format for transferring data around. Here is an example:
{ "name" : "Niki"
, "age" : 30
, "likes" : ["guacamole", "coffee", "cats"]
, "hates" : [ "waiting" , "grapefruit"]
, "lunches" : [ {"day" : "monday", "loc" : "sweet green"}
, {"day" : "tuesday", "loc" : "stamp"}
, {"day" : "wednesday", "loc" : "farmers market"}
, {"day" : "thursday", "loc" : "lab"}
, {"day" : "friday", "loc" : "home"} ]
}In brief, each JSON object is either
a base value like a string, a number or a boolean,
an (ordered) array of objects, or
a set of string-object pairs.
Thus, we can encode (a subset of) JSON values with the datatype
> data JVal = JStr String
> | JNum Double
> | JBln Bool
> | JObj [(String, JVal)]
> | JArr [JVal]
> deriving (Eq, Ord, Show)Thus, the above JSON value would be represented by the JVal
> js1 =
> JObj [("name", JStr "Niki")
> ,("age", JNum 30)
> ,("likes", JArr [ JStr "guacamole", JStr "coffee", JStr "cats"])
> ,("hates", JArr [ JStr "waiting" , JStr "grapefruit"])
> ,("lunches", JArr [ JObj [("day", JStr "monday")
> ,("loc", JStr "sweet green")]
> , JObj [("day", JStr "tuesday")
> ,("loc", JStr "farmers market")]
> , JObj [("day", JStr "wednesday")
> ,("loc", JStr "farmers market")]
> , JObj [("day", JStr "thursday")
> ,("loc", JStr "lab")]
> , JObj [("day", JStr "friday")
> ,("loc", JStr "home")]
> ])
> ]Serializing Haskell values to JSON
Next, suppose that we want to write a small library to serialize Haskell values as JSON. We could write a bunch of functions like
> doubleToJSON :: Double -> JVal
> doubleToJSON = JNumsimilarly, we have
> stringToJSON :: String -> JVal
> stringToJSON = JStr
>
> boolToJSON :: Bool -> JVal
> boolToJSON = JBlnBut what about collections, namely objects and arrays? We might try
> doublesToJSON :: [Double] -> JVal
> doublesToJSON xs = JArr (map doubleToJSON xs)
>
> boolsToJSON :: [Bool] -> JVal
> boolsToJSON xs = JArr (map boolToJSON xs)
>
> stringsToJSON :: [String] -> JVal
> stringsToJSON xs = JArr (map stringToJSON xs)which of course, you could abstract by making the individual-element-converter a parameter
> xsToJSON :: (a -> JVal) -> [a] -> JVal
> xsToJSON f xs = JArr (map f xs)
>
> xysToJSON :: (a -> JVal) -> [(String, a)] -> JVal
> xysToJSON f kvs = JObj [ (k, f v) | (k, v) <- kvs ]but still, this is getting rather tedious, since we have to redefine versions for each Haskell type, and instantiate them by hand for each conversion
ghci> doubleToJSON 4
JNum 4.0
ghci> xsToJSON stringToJSON ["coffee", "guacamole", "cats"]
JArr [JStr "coffee",JStr "guacamole",JStr "cats"]
ghci> xysToJSON stringToJSON [("day", "monday"), ("loc", "zanzibar")]
JObj [("day",JStr "monday"),("loc",JStr "zanzibar")]and this gets more hideous when you have richer objects like
> lunches = [ [("day", "monday"), ("loc", "sweet green")]
> , [("day", "tuesday"), ("loc", "stamp")]
> , [("day", "wednesday"), ("loc", "farmers market")]
> , [("day", "thursday"), ("loc", "lab")]
> , [("day", "friday"), ("loc", "home")]
> ]because we have to go through gymnastics like
ghci> xsToJSON (xysToJSON stringToJSON) lunches
JArr [JObj [("day",JStr "monday"),("loc",JStr "sweet green")],JObj [("day",JStr "tuesday"),("loc",JStr "stamp")]]Ugh! So much for readability. Isn’t there a better way? Is it too much to ask for a magical toJSON that just works?
Type classes to the rescue!
Of course there is a better way, and the the route is paved by typeclasses!
Lets define a typeclass that describes any type that can be converted to JSON.
> class JSON a where
> toJSON :: a -> JValEasy enough. Now, we can make all the above instances of JSON like so
> instance JSON Double where
> toJSON = JNum
>
> instance JSON Bool where
> toJSON = JBln
>
> instance JSON String where
> toJSON = JStrNow, we can just say
ghci> toJSON 4
JNum 4.0
ghci> toJSON True
JBln True
ghci> toJSON "guacamole"
JStr "guacamole"Bootstrapping Instances
The real fun begins when we get Haskell to automatically bootstrap the above functions to work for lists and association lists!
> instance {-# OVERLAPS #-} JSON a => JSON [a] where
> toJSON xs = JArr [toJSON x | x <- xs]Whoa!
The above says, if a is an instance of JSON, that is, if you can convert a to JVal then here’s a generic recipe to convert lists of a values!
ghci> toJSON [True, False, True]
JArr [JBln True,JBln False,JBln True]
ghci> toJSON ["cat", "dog", "Mouse"]
JArr [JStr "cat",JStr "dog",JStr "Mouse"]
ghci> toJSON [["cat", "dog"], ["mouse", "rabbit"]]
JArr [JArr [JStr "cat",JStr "dog"],JArr [JStr "mouse",JStr "rabbit"]]Of course, we can pull the same trick with key-value lists
> instance (JSON a) => JSON [(String, a)] where
> toJSON kvs = JObj [ (k, toJSON v) | (k, v) <- kvs ]after which, we are all set!
ghci> toJSON lunches
JArr [JObj [("day",JStr "monday"),("loc",JStr "stamp")],JObj [("day",JStr "tuesday"),("loc",JStr "stamp")]]It is also useful to bootstrap the serialization for tuples (upto some fixed size) so we can easily write “non-uniform” JSON objects where keys are bound to values with different shapes.
> instance (JSON a, JSON b) => JSON ((String, a), (String, b)) where
> toJSON ((k1, v1), (k2, v2)) =
> JObj [(k1, toJSON v1), (k2, toJSON v2)]
>
> instance (JSON a, JSON b, JSON c) => JSON ((String, a), (String, b), (String, c)) where
> toJSON ((k1, v1), (k2, v2), (k3, v3)) =
> JObj [(k1, toJSON v1), (k2, toJSON v2), (k3, toJSON v3)]
>
> instance (JSON a, JSON b, JSON c, JSON d) => JSON ((String, a), (String, b), (String, c), (String,d)) where
> toJSON ((k1, v1), (k2, v2), (k3, v3), (k4, v4)) =
> JObj [(k1, toJSON v1), (k2, toJSON v2), (k3, toJSON v3), (k4, toJSON v4)]
>
> instance (JSON a, JSON b, JSON c, JSON d, JSON e) => JSON ((String, a), (String, b), (String, c), (String,d), (String, e)) where
> toJSON ((k1, v1), (k2, v2), (k3, v3), (k4, v4), (k5, v5)) =
> JObj [(k1, toJSON v1), (k2, toJSON v2), (k3, toJSON v3), (k4, toJSON v4), (k5, toJSON v5)]Now, we can simply write
> hs = (("name" , "Niki")
> ,("age" , 30 :: Double)
> ,("likes" , ["guacamole", "coffee", "cats"])
> ,("hates" , ["waiting", "grapefruit"])
> ,("lunches", lunches)
> )which is a Haskell value that describes our running JSON example, and can convert it directly like so
> js2 = toJSON hsThis value is exactly equal to the old “hand-serialized” JSON object js1.
ghci> js1 == js2
TrueThats it for today. We will see much more typeclass awesomeness in the next few lectures…