Monoids & Foldables (& Kinds)

This lecture is adjusted from Learn you a Haskell for Great Good!.

Haskell’s combination of purity, higher order functions, parameterized algebraic data types, and typeclasses allows us to implement polymorphism on a much higher level than possible in other languages. It allows us to abstract over properties of functions (what we call class lows)! We don’t have to think about types belonging to a big hierarchy of types. Instead, we think about what the types can act like and then connect them with the appropriate typeclasses. An Int can act like a lot of things. It can act like an equatable thing, like an ordered thing, like an enumerable thing, etc.

Typeclasses are open, which means that we can define our own data type, think about what it can act like and connect it with the typeclasses that define its behaviors. Because of that and because of Haskell’s great type system that allows us to know a lot about a function just by knowing its type declaration, we can define typeclasses that define behavior that’s very general and abstract (using terminology from the scary Category Theory). We’ve met typeclasses that define operations for seeing if two things are equal,comparing two things by some ordering or turning things into a JSon. Those are very abstract and elegant behaviors, but we just don’t think of them as anything very special because we’ve been dealing with them for most of our lives. Our goal in the next lectures it to understand the abstract class of Monads. The path to Monads goes throught the classes of functors and applicatives. But let’s start today with a simpler class: monoids, which are sort of like socks.

> 
> {-# LANGUAGE FlexibleInstances #-}
> 
> module MonoidsAndFoldables where
> 
> import Data.Monoid   hiding (Any(..), All(..), Sum(..))
> import Data.Foldable hiding (sum)
> import Prelude       hiding (sum)

Monoids

Type classes in Haskell are used to present an interface for types that have some behavior in common. We started out with simple type classes like Eq, which is for types whose values can be equated, and Ord, which is for things that can be put in an order and then moved on to more interesting ones.

When we make a type, we think about which behaviors it supports, i.e. what it can act like and then based on that we decide which type classes to make it an instance of. If it makes sense for values of our type to be equated, we make it an instance of the Eq type class.

Now consider the following: (*) is a function that takes two numbers and multiplies them. If we multiply some number with an 1, the result is always equal to that number. It doesn’t matter if we do 1 * x or x * 1, the result is always x. Similarly, (++) is also a function which takes two things and returns a third. Only instead of multiplying numbers, it takes two lists and concatenates them. And much like (*), it also has a certain value which doesn’t change the other one when used with (++). That value is the empty list: [].

ghci> 4 * 1  
4  
ghci> 1 * 9  
9  
ghci> [1,2,3] ++ []  
[1,2,3]  
ghci> [] ++ [0.5, 2.5]  
[0.5,2.5]

It seems that both (*) together with 1 and (++) along with [] share some common properties.

Q: Can you write down the common properties in Haskell terms?

(Multiplication , 1 )

x ++ [] = x 
[] ++ x = x
x ++ (y ++ z) = (x ++ y) ++ z 

x * y == y * x

There’s another thing that these two operations have in common that may not be as obvious as our previous observations: when we have three or more values and we want to use the binary function to reduce them to a single result, the order in which we apply the binary function to the values doesn’t matter. It doesn’t matter if we do (3 * 4) * 5 or 3 * (4 * 5). Either way, the result is 60. The same goes for (++):

ghci> (3 * 2) * (8 * 5)  
240  
ghci> 3 * (2 * (8 * 5))  
240  
ghci> "la" ++ ("di" ++ "da")  
"ladida"  
ghci> ("la" ++ "di") ++ "da"  
"ladida"

We call this property associativity. (*) is associative, and so is (++), but (-), for example, is not. The expressions (5 - 3) - 4 and 5 - (3 - 4) result in different numbers.

By noticing and writing down these properties, we have chanced upon monoids! A monoid is when you have an associative binary function and a value which acts as an identity with respect to that function. When something acts as an identity with respect to a function, it means that when called with that function and some other value, the result is always equal to that other value. 1 is the identity with respect to (*) and ([]) is the identity with respect to (++). There are a lot of other monoids to be found in the world of Haskell, which is why the Monoid type class exists. It’s for types which can act like monoids. Let’s see how the type class is defined:

class Monoid m where  
    mempty  :: m  
    mappend :: m -> m -> m  
    mconcat :: [m] -> m  
    mconcat = foldr mappend mempty

The Monoid type class is defined in import Data.Monoid. Let’s take some time and get properly acquainted with it.

The first function is mempty. It’s not really a function, since it doesn’t take parameters, so it’s a polymorphic constant, kind of like minBound from Bounded. mempty represents the identity value for a particular monoid.

Next up, we have mappend, which, as you’ve probably guessed, is the binary function. It takes two values of the same type and returns a value of that type as well. It’s worth noting that the decision to name mappend as it’s named was kind of unfortunate, because it implies that we’re appending two things in some way. While (++) does take two lists and append one to the other, (*) doesn’t really do any appending, it just multiplies two numbers together. When we meet other instances of Monoid, we’ll see that most of them don’t append values either, so avoid thinking in terms of appending and just think in terms of mappend being a binary function that takes two monoid values and returns a third.

The last function in this type class definition is the default function mconcat. It takes a list of monoid values and reduces them to a single value by doing mappend between the list’s elements. It has a default implementation, which just takes mempty as a starting value and folds the list from the right with mappend. Because the default implementation is fine for most instances, we won’t concern ourselves with mconcat too much from now on. When making a type an instance of Monoid, it suffices to just implement mempty and mappend.

Q: Can you think of a reason why we would not use the default implementation of mconat?

Monoid Laws

Before moving on to specific instances of Monoid, let’s take a brief look at the monoid laws. We mentioned that there has to be a value that acts as the identity with respect to the binary function and that the binary function has to be associative. It’s possible to make instances of Monoid that don’t follow these rules, but such instances are of no use to anyone because when using the Monoid type class, we rely on its instances acting like monoids. Otherwise, what’s the point? That’s why when making instances, we have to make sure they follow these laws:

mempty `mappend` x = x
x `mappend` mempty = x
(x `mappend` y) `mappend` z = x `mappend` (y `mappend` z)

The first two state that mempty has to act as the identity with respect to mappend and the third says that mappend has to be associative i.e., that it the order in which we use mappend to reduce several monoid values into one doesn’t matter. Haskell doesn’t enforce these laws, so we as the programmer have to be careful that our instances do indeed obey them.

Lists are monoids

Yes, lists are monoids! Like we’ve seen, the (++) function and the empty list [] form a monoid. The instance is very simple:

instance Monoid [a] where  
    mempty  = []  
    mappend = (++)

Lists are an instance of the Monoid type class regardless of the type of the elements they hold.

Giving this a test run, we encounter no surprises:

ghci> [1,2,3] `mappend` [4,5,6]  
[1,2,3,4,5,6]  
ghci> ("one" `mappend` "two") `mappend` "tree"  
"onetwotree"  
ghci> "one" `mappend` ("two" `mappend` "tree")  
"onetwotree"  
ghci> "one" `mappend` "two" `mappend` "tree"  
"onetwotree"  
ghci> "pang" `mappend` mempty  
"pang"  
ghci> mconcat [[1,2],[3,6],[9]]  
[1,2,3,6,9]

Q: What is the type of mempty?

Note on associativity: Using mappend as an infix operator saves parethesis! The following

mappend "123" mappend "234" "33"

attempts to pass the second mappend as an argument to the first leading to a weird type error! There are two solutions, either use the dollar operator or use mappend as an infix operator.

Haskell defaults infix operators to be left associative, that is the following two expressions are equal

"one" `mappend` "two" `mappend` "tree" 
("one" `mappend` "two") `mappend` "tree"

Haskell it up! Even when using mappend as infix the code has too many characters for a Haskell program. To save up characters the Monoid library provides an infix operator (<>) that acts exactly like mappend.

infixr 6 <>
(<>) :: Monoid m => m -> m -> m
(<>) = mappend

Using (<>) now we can instead write

ghci> "one" <> "two" <> "tree"

saving 7 characters at each mappend call!

To use mempty as the monoid list identity we have to write an explicit type annotation, because if we just did mempty, GHCi wouldn’t know which instance to use, so we had to say we want the list instance. We were able to use the general type of [a] (as opposed to specifying [Int] or [String]) because the empty list can act as if it contains any type.

Because mconcat has a default implementation, we get it for free when we make something an instance of Monoid! In the case of the list, mconcat turns out to be just concat. It takes a list of lists and flattens it, because that’s the equivalent of doing (++) between all the adjecent lists in a list.

Q: Do the monoid laws hold for the list instance?

Assumption 
[] ++ xs = xs 
(y:ys) ++ xs = y:(ys ++ xs)
GOAL: [] ++ xs = xs 
-- trivial 
GOAL: xs ++ [] = xs 
-- by structural induction 

[]     ++ [] = [] 
(x:xs) ++ [] = x:(xs++[])
                 --  Inductive Hypothesis
                 = x:xs

Notice that monoids don’t require that a <> b be equal to b <> a. In the case of the list, they clearly aren’t:

ghci> "one" <> "two"  
"onetwo"  
ghci> "two" <> "one"  
"twoone"

And that’s okay. The fact that for multiplication 3 * 5 and 5 * 3 are the same is just a property of multiplication, but it doesn’t hold for all (and indeed, most) monoids. In fact, we call the monoids that satisfy the property x <> y == y <> x commutative monoids.

The newtype keyword

We already examined one way for numbers to be considered monoids. Just have the binary function be (*) and the identity value 1. It turns out that that’s not the only way for numbers to be monoids!

Q: Can you think of another famous binary operator on numbers with an identity element?

Another way is to have the binary function be (+) and the identity value 0:

ghci> 0 + 4  
4  
ghci> 5 + 0  
5  
ghci> (1 + 3) + 5  
9  
ghci> 1 + (3 + 5)  
9

The monoid laws hold, because if you add 0 to any number, the result is that number. And addition is also associative, so we get no problems there. So now that there are two equally valid ways for numbers to be monoids, which way do choose? Well, we don’t have to.

We can use the newtype keyword to define multiple monoid instances for numbers!

So far, we’ve learned how to make our own algebraic data types by using the data keyword. We’ve also learned how to give existing types synonyms with the type keyword. Now, we’ll be taking a look at how to make new types out of existing data types by using the newtype keyword and why we’d want to do that in the first place.

To be able to use numbers as monoids both on (*) and (+) we can define two different data types that wrap numbers.

data Prods = Prods {getProd :: Int} 
data Sums  = Sums  {getSum  :: Int}

We defined two data types that have just one value constructor and that value constructor has just one field that is a list of things.

The newtype keyword in Haskell is made exactly the cases when we want to just take one type and wrap it in something to present it as another type. In a real application, Prods and Sums would be defined like this:

newtype Prods = Prods {getProd :: Int} 
newtype Sums  = Sums  {getSum  :: Int}

Instead of the data keyword, the newtype keyword is used. Now why is that? Well for one, newtype is faster. If you use the data keyword to wrap a type, there’s some overhead to all that wrapping and unwrapping when your program is running. But if you use newtype, Haskell knows that you’re just using it to wrap an existing type into a new type (hence the name), because you want it to be the same internally but have a different type. With that in mind, Haskell can get rid of the wrapping and unwrapping once it resolves which value is of what type.

So why not just use newtype all the time instead of data then? Well, when you make a new type from an existing type by using the newtype keyword, you can only have one value constructor and that value constructor can only have one field. But with data, you can make data types that have several value constructors and each constructor can have zero or more fields:

data Tile = X | O | EmptyTile

When using newtype, you’re restricted to just one constructor with one field.

We can also use the deriving keyword with newtype just like we would with data. We can derive instances for Eq, Ord, and Show. If we derive the instance for a type class, the type that we’re wrapping has to be in that type class to begin with. It makes sense, because newtype just wraps an existing type. So now if we do the following, we can print and equate values of our new type:

> newtype Prods = Prods {getProd :: Int} deriving (Eq, Ord, Show) 
> newtype Sums  = Sums  {getSum  :: Int} deriving (Eq, Ord, Show)

Let’s give that a go:

ghci> Prods 42
Prods {getProd = 42}
ghci> Prods 42 == Prods  42  
True  
ghci> Prods 42 <  Prods  42
False

In this particular newtype, the value constructor has the following type:

Prods :: Int -> Prods

It takes an Int value, such as 42 and returns a Prods value. From the above examples where we used the Prods value constructor, we see that really is the case. Conversely, the getProd function, which was generated for us because we used record syntax in our newtype, has this type:

getProd :: Prods -> Int

It takes a Prods value and converts it to an Int value. You can think of this as wrapping and unwrapping, but you can also think of it as converting values from one type to the other.

On newtype laziness

We mentioned that newtype is usually faster than data. The only thing that can be done with newtype is turning an existing type into a new type, so internally, Haskell can represent the values of types defined with newtype just like the original ones, only it has to keep in mind that the their types are now distinct. This fact means that not only is newtype faster, it’s also lazier. Let’s take a look at what this means.

Haskell is lazy by default, which means that only when we try to actually print the results of our functions will any computation take place. Furthemore, only those computations that are necessary for our function to tell us the result will get carried out. The undefined value in Haskell represents an erronous computation. If we try to evaluate it (that is, force Haskell to actually compute it) by printing it to the terminal, Haskell will throw a hissy fit (technically referred to as an exception):

ghci> undefined  
*** Exception: Prelude.undefined

However, if we make a list that has some undefined values in it but request only the head of the list, which is not undefined, everything will go smoothly because Haskell doesn’t really need to evaluate any other elements in a list if we only want to see what the first element is:

ghci> head [3,4,5,undefined,2,undefined]  
3

Now consider the following type:

> data DataBool = DataBool { getDataBool :: Bool }

It’s your run-of-the-mill algebraic data type that was defined with the data keyword. It has one value constructor, which has one field whose type is Bool. Let’s make a function that pattern matches on a DataBool and returns the value “hello” regardless of whether the Bool inside the DataBool was True or False:

> helloMe :: DataBool -> String  
> helloMe (DataBool _) = "hello"

Instead of applying this function to a normal DataBool, let’s throw it a curveball and apply it to undefined!

ghci> helloMe undefined  
*** Exception: Prelude.undefined

Yikes! An exception! Now why did this exception happen? Types defined with the data keyword can have multiple value constructors (even though DataBool only has one). So in order to see if the value given to our function conforms to the (DataBool _) pattern, Haskell has to evaluate the value just enough to see which value constructor was used when we made the value. And when we try to evaluate an undefined value, even a little, an exception is thrown.

Instead of using the data keyword for NewTypeBool, let’s try using newtype:

> newtype NewTypeBool = NewTypeBool { getCoolBool :: Bool }

Let’s now use NewTypeBool to define again the helloMe function.

> helloMe' :: NewTypeBool -> String  
> helloMe' (NewTypeBool _) = "hello"

Let’s do the same thing here and apply helloMe' to an undefined value:

ghci> helloMe' undefined  
"hello"

Q: It worked! Hmmm, why is that?

Well, like we’ve said, when we use newtype, Haskell can internally represent the values of the new type in the same way as the original values. It doesn’t have to add another box around them, it just has to be aware of the values being of different types. And because Haskell knows that types made with the newtype keyword can only have one constructor, it doesn’t have to evaluate the value passed to the function to make sure that it conforms to the (NewTypeBool _) pattern because newtype types can only have one possible value constructor and one field!

This difference in behavior may seem trivial, but it’s actually pretty important because it helps us realize that even though types defined with data and newtype behave similarly from the programmer’s point of view because they both have value constructors and fields, they are actually two different mechanisms. Whereas data can be used to make your own types from scratch, newtype is for making a completely new type out of an existing type. Pattern matching on newtype values isn’t like taking something out of a box (like it is with data), it’s more about making a direct conversion from one type to another.

type vs. newtype vs. data

At this point, you may be a bit confused about what exactly the difference between type, data and newtype is, so let’s refresh our memory a bit.

> type Move = (Int,Int)

All this does is to allow us to refer to the (Int,Int) type as Move. They can be used interchangeably. We don’t get an Move value constructor or anything like that. Because Move and (Int,Int) are only two ways to refer to the same type, it doesn’t matter which name we use in our type annotations:

ghci> ((1,2) :: Move) < ((3,4) :: (Int,Int))  
True

We use type synonyms when we want to make our type signatures more descriptive by giving types names that tell us something about their purpose in the context of the functions where they’re being used.

newtype Move = Move { getMove :: (Int,Int) }

We can’t use (<) to compare Move with (Int,Int) We cannot even compare Move with Move unless we define an Ord instance on Move.

When we use record syntax in our newtype declarations, we get functions for converting between the new type and the original type: namely the value constructor of our newtype and the function for extracting the value in its field. The new type also isn’t automatically made an instance of the type classes that the original type belongs to, so we have to derive or manually write the same or a new instance.

In practice, you can think of newtype declarations as data declarations that can only have one constructor and one field. If you catch yourself writing such a data declaration, consider using newtype.

If you just want your type signatures to look cleaner and be more descriptive, you probably want type synonyms. If you want to take an existing type and wrap it in a new type in order to make it an instance of a type class, chances are you’re looking for a newtype. And if you want to make something completely new, odds are good that you’re looking for the data keyword.

Using newtype to make type class instances

Now that we know all about newtype, lets go back to monoids on numbers! We use newtype to define multiple instances of the same type class for the same type: we can wrap that type in a newtype and then make the new type an instance of the type class in a different way. We can have our cake and eat it too.

The Data.Monoid module exports two types for this, namely Product and Sum. Product is defined like this:

> newtype Sum a =  Sum { getSum' :: a }  
>     deriving (Eq, Ord, Read, Show)  
> 
> instance Num a => Monoid (Sum a) where  
>     mempty = Sum 0
>     Sum x `mappend` Sum y = Sum (x + y)

False || x == x x || False == x x || (y || z) == (x || y) || z

> newtype Any a =  Any {  getAny :: a }  
>     deriving (Eq, Ord, Read, Show)  
> 
> instance Monoid (Any Bool) where  
>     mempty = Any False
>     Any x `mappend` Any y = Any (x || y)      
newtype Product a =  Product { getProduct :: a }  
    deriving (Eq, Ord, Read, Show)

Simple, just a newtype wrapper with one type parameter along with some derived instances. Its instance for Monoid goes a little something like this:

instance Num a => Monoid (Product a) where  
    mempty = Product 1  
    Product x `mappend` Product y = Product (x * y)

mempty is just 1 wrapped in a Product constructor. mappend pattern matches on the Product constructor, multiplies the two numbers and then wraps the resulting number back. As you can see, there’s a Num a class constraint. So this means that Product a is an instance of Monoid for all a’s that are already an instance of Num.

Q: We saw that we can use (<>) instead of mappend to append monoids. Can we use (<>) instead of mappend in the monoid instance definition?

To use Product a as a monoid, we have to do some newtype wrapping and unwrapping:

ghci> getProduct $ Product 3 <> Product 9  
27  
ghci> getProduct $ Product 3 <> mempty  
3  
ghci> getProduct $ Product 3 <> Product 4 <> Product 2  
24  
ghci> getProduct . mconcat . map Product $ [3,4,2]  
24

This is nice as a showcase of the Monoid type class, but no one in their right mind would use this way of multiplying numbers instead of just writing 3 * 9 and 3 * 1. But a bit later, we’ll see how these Monoid instances that may seem trivial at this time can come in handy.

Q: Define Sum and its monoid instance like Product so that

ghci> getSum $ Sum 2 <> Sum 9  
11  
ghci> getSum $ mempty <> Sum 3  
3  
ghci> getSum . mconcat . map Sum $ [1,2,3]  
6  
newtype Product a =  Product { getProduct :: a }  
    deriving (Eq, Ord, Read, Show)

Simple, just a newtype wrapper with one type parameter along with some derived instances. Its instance for Monoid goes a little something like this:

instance Num a => Monoid (Product a) where  
    mempty = Product 1  
    Product x `mappend` Product y = Product (x * y)

Any and All

Another type which can act like a monoid in two distinct but equally valid ways is Bool. The first way is to have the or function (||) act as the binary function along with False as the identity value. The way or works in logic is that if any of its two parameters is True, it returns True, otherwise it returns False. So if we use False as the identity value, it will return False when or-ed with False and True when or-ed with True.

Q: Let’s define an Any new type and its Monoid instance, so that

ghci> getAny $ Any True <> Any False  
True  
ghci> getAny $ mempty <> Any True  
True  
ghci> getAny . mconcat . map Any $ [False, False, False, True]  
True  
ghci> getAny $ mempty <> mempty  
False

The other way for Bool to be an instance of Monoid is to kind of do the opposite: have (&&) be the binary function and then make True the identity value. Logical and will return True only if both of its parameters are True. This is the newtype declaration, nothing fancy:

Q: Let’s define an All new type and its Monoid instance, so that

ghci> getAll $ mempty <> All True  
True  
ghci> getAll $ mempty <> All False  
False  
ghci> getAll . mconcat . map All $ [True, True, True]  
True  
ghci> getAll . mconcat . map All $ [True, True, False]  
False

Just like with multiplication and addition, we usually explicitly state the binary functions instead of wrapping them in newtypes and then using mappend and mempty. mconcat seems useful for Any and All, but usually it’s easier to use the or and and functions, which take lists of Bools and return True if any of them are True or if all of them are True, respectively.

Using monoids to fold data structures

One of the more interesting ways to put monoids to work is to make them help us define folds over various data structures. So far, we’ve only done folds over lists, but lists aren’t the only data structure that can be folded over. We can define folds over almost any data structure. As you will see in your homework, Trees lend themselves well to folding.

Because there are so many data structures that work nicely with folds, the Foldable type class was introduced. Folds can be found in Data.Foldable and because it export functions whose names clash with the ones from the Prelude, it’s best imported qualified (and served with basil):

import qualified Data.Foldable as F

To save ourselves precious keystrokes, we’ve chosen to import it qualified as F.

Alright, so what are some of the functions that this type class defines?

When we introduced recusion over lists, we saw the functions foldl and length, But what are the real types of these functions?

Well, among them are foldr, foldl, foldr1 and foldl1. Huh? But we already know these functions, what’s so new about this? Let’s compare the types of Foldable’s foldr and the foldr from the Prelude to see how they differ:

ghci> :t length  
length :: Foldable t => t a -> Int
ghci> :t foldl
foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b

Parenthesis: Kind System

Wait! What does t a mean?

Q: What does a mean?

We are used to abstract over types, but in Haskell we can further abstarct over type constuctors. A type constructor constructs types, given a type, it returns another type. Much like functions (eg id) that given an expression it returns another expression. For example, t above can be instantiated to Maybe, Prod, Sum, [], etc. But cannot get instantiated to Bool, Int, Maybe Int, etc

Q: Can t be instantiated to Assoc?

> data Assoc k v = Tip | Bin k v (Assoc k v) (Assoc k v)
>   deriving (Show, Eq)

The compiler decides the good instances of t using a kind system. As values have types, types have kinds. The kind * represents the all types of values (the universe).

ghci> :k Int
Int :: *
ghci> :k Bool
Bool :: *
ghci> :k Maybe Int
Maybe Int :: *

Lets figure out more interesting kinds. What is the kind of Maybe, All, Assoc, Monoid, Foldable?

The kind system tell us what instances we can create.

Q: Which of the following “kind”-check?

instance Monoid   Int   where
instance Monoid   Maybe where
instance Monoid   Assoc where
instance Foldable Int   where
instance Foldable Maybe where
instance Foldable Assoc where

The kind system allows for quite fancy (i.e., higher order) operations like currying and higher order kinds.

Q: What is the kind of Assoc Int, forall a. Assoc a, IHaveFunctionKind?

> data IHaveFunctionKind t a = IHFK (a -> t a -> Bool)

In short, the expressive kind system allows for “type level programming” or dependent types. Who needs terms, anyway?

Closing Parenthesis: Back to Foldables

Ah! So length and foldl is not defined only over lists, but instead over any type that can be folded up! Okay then, what are some other data structures that support folds? Well, there’s the Maybe we all know and love!

ghci> foldl (+) 2 (Product 42)  
44
ghci> length (Product 42) 
1

Combining folds and monoids we get the foldMap function, which is also a part of the Foldable type class. The foldMap function has the following type:

foldMap :: (Monoid m, Foldable t) => (a -> m) -> t a -> m

Its first parameter is a function that takes a value of the type that our foldable structure contains (denoted here with a) and returns a monoid value. Its second parameter is a foldable structure that contains values of type a. It maps that function over the foldable structure, thus producing a foldable structure that contains monoid values. Then, by doing mappend between those monoid values, it joins them all into a single monoid value. This function may sound kind of odd at the moment, but we’ll see that it’s very easy to implement. What’s also cool is that implementing this function is all it takes for our type to be made an instance of Foldable. So if we just implement foldMap for some type, we get length, foldr and foldl on that type for free!

Q: Define the Foldable instance for the below List type.

> data List a = N | C a (List a)

Now we get all the folding functions for free! Assuming a test toy list

> testList = [1, 42, 12]

You can fold it or get its legth.

ghci> foldl (+) 0 testList
55  
ghci> foldl (*) 1 testList  
504

And also, foldMap isn’t only useful for making new instances of Foldable; it comes in handy for reducing our structure to a single monoid value. For instance, if we want to know if any number in our tree is equal to 42, we can do this:

ghci> getAny $ foldMap (\x -> Any $ x == 42) testList

Here, \x -> Any $ x == 3 is a function that takes a number and returns a monoid value, namely a Bool wrapped in Any. foldMap applies this function to every element in our tree and then reduces the resulting monoids into a single monoid with mappend.

Q: What is the value of

ghci> getAny $ foldMap (\x -> Any $ x > 15) testList

Q: What is the value of

ghci> foldMap (\x -> [x]) testList

What’s cool is that all of these trick aren’t limited to the List, they work on any instance of Foldable.

foldMap = mapReduce

foldMap might be a function difficult to digest, but as we shall now see it is the heart of the more famous function mapReduce.

alt text

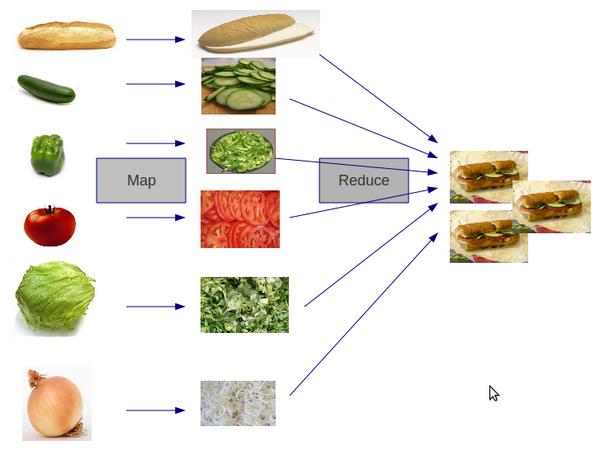
alt text

MapReduce applies a function f to its input in parallel.

Note that combining or reducing the mapped chunks is called folding in the functional world. Thus, mapReduce is basically foldMap, if only we had a chunking function.

Let’s then use the type class magic to define our missing component, a chunk function.

We define a class Chunkable with a methos that chunks its arguments into a list.

> class Chunkable a where 
>   chunk :: a -> [a]

For example, a list is a Chunkable chunking its input list to lists of lists of length at most 2.

> instance Chunkable [a] where
>   chunk x | length x <= 2 = [x]
>   chunk x = take 2 x: chunk (drop 2 x)

Now that we have chunk we can define mapReduce in terms of foldMap

> mapReduce :: (Chunkable a, Monoid b) 
>           => (a -> b) -> (a -> b)
> mapReduce f x = foldMap f (chunk x)

First chunk the input and then foldMap the input function f into each chunk!

Lets see a use case of mapReduce We define the sum of an integer list to return the Sum of its elements. Since Sum Int is a Monoid we can already use the mconat monoid operation

sum :: [Int] -> Sum Int 
sum = mconcat . map Sum

This just works!

ghc> sum [1..100]
Sum {getSum = 5050}

Since the input of sum is a list (a.k.a. Chunkable) and its result is a Monoid we can apply it to mapReduce:

psum :: [Int] -> Sum Int 
psum = mapReduce sum

Unexpectedly, sum and psum behave the same:

ghc> sum [1..100]
Sum {getSum = 5050}

So, what did we get? Looking closely at the type of mapRecude, it merely tranforms a function f :: a -> b to a function from a -> b. Due to polymorphism the result function is equivalnt to the input one. So, we got nothing!

Q: Is this even true? Can you construct a mapReduceBad implementation with the same type as mapReduce that returns a non-equivalent function?

> mapReduceBad :: (Chunkable a, Monoid b) 
>              => (a -> b) -> (a -> b)
> mapReduceBad f x = mempty
> 
> id' :: Monoid a => a -> a 
> id' x = mempty

Ok, assuming that the returning function behaves as the input one, what did you get? Nothing for now, but in a pure function like Hakell the map portion of foldMap can get parallelised, and then we got efficiency!

Project Idea: Define the mapReducable type class and use it to (actually) parallelize divide and conquer algorithms, for example string matching.

Summary

Monoids are a class of functions defined in abstract algebra that satisfy special properties.

In this lecture we learnt two important lessons.

Let’s now go and two equally important type classes, Functors and Applicatives.